CUSUMTESTS Procedure

@CusumTests performs performs CUSUM and CUSUMQ tests from Brown, Durbin & Evans(1975) on the input series, which should be a series of recursive residuals. The significance level on the CUSUM test is from Zeileis(2004), while the critical boundaries for the CUSUMQ test is from Edgerton & Wells(1994).

@CusumTests( options )resids start end

Options

FOOTER="graph footer" ["CUSUM Tests"]

HEADER="graph header" [none]

Variables Defined

%CDSTAT	value of the CUSUM statistic (maximum absolute value) (REAL)
%SIGNIF	(approximate) significance level of the CUSUM (REAL)
%%CUSUMQ	value of CUSUMQ statistic (maximum absolute gap) (REAL)
%%CUSUMQCV	.05 critical value for CUSUMQ (REAL)

Example

* Baltagi, Econometrics, 3rd edition

* CUSUM test from p 201

open data consump.dat

cal(a) 1950

data(format=prn,org=columns) 1950:1 1993:1

rls(csum=cusum,csquared=cusumsq,dfhist=dfs) c / rresids

# constant y

* CUSUM test. The CUSUMTests procedure does both the CUSUM and the

* CUSUMQ (squared) tests taking a set of recursive residuals as the

* input.

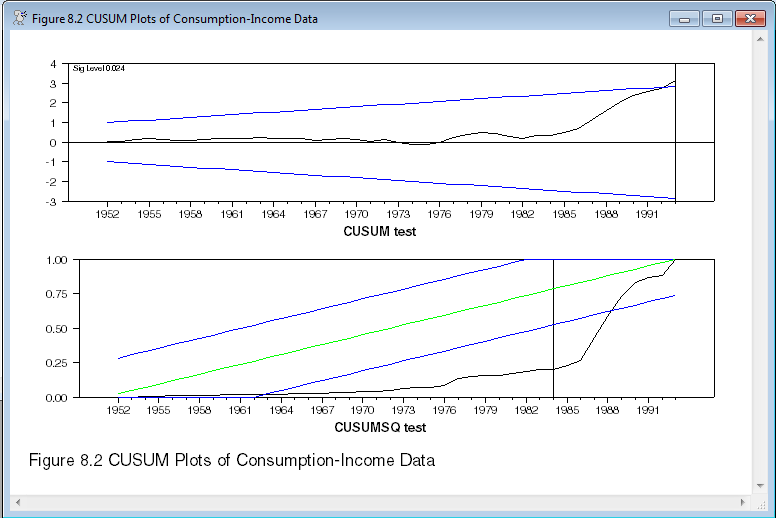
@CusumTests(footer="Figure 8.2 CUSUM Plots of Consumption-Income Data") rresids

Sample Output

The top graph is the CUSUM test, which tests primarily for a break in the model itself, and the CUSUMSQ test which tests primarily for a break in the residual variance. The vertical lines mark the largest deviation. The expected value for the CUSUM is zero, while for CUSUMSQ, it's the green line. In both cases, the blue lines show the .05 limits for deviations. The CUSUM test seems to indicate a possible problem right near the end of the data, while the CUSUMSQ test rather strongly rejects model stability.