Diebold Yilmaz spillover papers |
In a pair of papers, Diebold and Yilmaz(2009, 2012) proposed calculation of "spillover" indexes by examining the decomposition of variance (in 2009) and a "generalized" decomposition of variance (2012) for a VAR on a large set of series and aggregating them into "to" and "from" measures for flow of variance. The basic calculation is the same for each: however, the 2009 paper uses a standard Cholesky factorization (which is sensitive to ordering—part of the paper examines the robustness to changes in the ordering), while the 2012 paper bases the calculation on "generalized" impulse responses rather than an actual factorization. While the latter isn't sensitive to ordering, it produces a decomposition of a quantity which has no real economic interpretation, while the Cholesky factorization is decomposing the actual forecast error variances of the series.
The DY papers have proven very popular, which has generated quite a few questions about extensions of the technique. It’s important to understand what this can and can't do. If one looks at the original 2009 paper, it repackaged standard decompositions of variance for a very large set of (similar) series. If, instead, you have a more modest-sized structural model, you can just use the standard FEVD's directly—aggregating into "from" and "to" doesn’t even make sense when the shocks don't correspond one-to-one with the variables. If you have a more structured model of the contemporaneous interaction, your shocks will typically be interpreted as things like "supply", "demand", "monetary policy", which don't have any obvious direct relationship with the series and which neither have nor need any aggregation across groupings of shocks.
The principal innovation in the 2012 paper is the use of "generalized impulse responses" rather than conventional Cholesky shocks. To demonstrate, suppose the covariance matrix in a two-variable VAR is
![]()
which has a high positive correlation (.8). If these were two relatively "equal" countries, and one did not want to try to come up with a structural model to explain the high correlation, it would be difficult to justify choosing one country to be "first". The standard Cholesky factors in the two orders are
![]()
With order 1-2, the first step variance for variable 1 is 100% assigned to its own shock, while in the order 2-1,it’s 2.56/4.00 (or 64%) assigned to the second variable and 36% to the first. The DY generalized spillover calculation is to (in effect), use column 1 from the matrix on the left and column 2 from the matrix on the right and compute the share of variable 2 for variable 1 as
![]()
While this is a relatively straightforward calculation, it’s not clear what the denominator in this means—it pulls numbers out of two only loosely related matrices. An alternative computation which is similarly not sensitive to ordering (but, unfortunately is not feasible above about five variables) would be to average the decompositions across all possible Cholesky factors. That would give you a 68%-32% breakdown. In the two-variable case, the difference between the two calculations is that averaging would include 1.22 as an additional term in the denominator (so the denominator would have two full variance calculations). The DY calculation will be biased upwards on the "other" variables.
If you're doing the DY calculations, you can choose between the Cholesky and generalized calculations by changing:
compute usegirf=0
If USEGIRF is 0, the Cholesky factor is used, otherwise, the generalized calculations are done.
Number of Steps
Both papers use calculations of responses at 10 steps ahead (for the Cholesky shocks, this means the decomposition of variance of 10 step forecasts), which is governed by the instruction
compute nsteps=10
The 2009 paper uses weekly data and the 2012 uses daily, so the 10 isn't chosen to represent a certain amount of time. The 2009 paper also looks at 2 steps, while the 2012 paper looks at sensitivity to choices of this, graphing the ranges from 5 to 10. At any rate, you don't want it to be too large, as the longer term impulse responses tend to be dominated by just one or two roots, even for stationary processes.
Stable Roots
The 2009 paper examines two different collection of series: returns and volatility. Returns (as is typical) have relatively low serial correlation. Volatility, on the other hand, is fairly persistent. In the rolling sample estimates, the paper chose to skip over any data points where the estimated VAR had unstable roots. (They will show in graphs as dotted lines connecting the entries without a problem). The explanation was that the unstable roots caused the results to be out-of-line with nearby data points without unstable roots. To give you an option of including them anyway, we added a control
compute skipUnstable=1
If you change it to skipUnstable=0, it will include all the data points, regardless of the roots of the VAR.
Rolling Sample Span
Both papers include a "rolling sample" analysis, re-estimating the statistics using repeated estimations over nested subsamples. Both papers use a 200 period window, while the 2009 paper also does a 75 week window. A common error in doing rolling samples is to pick a window which is too small for the size of the model. The 75 period window with the 2009 data is probably, in practice, too short: with 19 variables and 2 lags that is using almost half the degrees of freedom.
Volatility Data
Both papers include an analysis of volatility data. These are computed from price data (which aren't included in the data set). The method used is shown in the VolatilityEstimates.rpf example program. Note that this is very different from what is done with a GARCH model, where the volatility is endogenous to the model.
Calculating Spillover Statistics
The RESULTS option for the ERRORS instruction saves the decomposition (in decimals) in a RECT[SERIES]. If you use RESULTS=GFEVD, then GFEVD(i,j) is a series running from entries 1 to NSTEPS with, at each step, the fraction of series i explained by shock j. The "cross-section" of that at entry NSTEPS can be pulled with %XT(GFEVD,NSTEPS), returning an \(m \times m\) array with variables in the rows and shocks in the columns. The various spillover measures will be sums of non-diagonal elements in this matrix. The rows represent the target variable, and the columns represent the shock variable. So the following, which sum either a row or column and subtract the diagonal, will give the spillover to and spillover from each variable.
dec vect tovar(%nvar) fromvar(%nvar)
ewise tovar(i)=%sum(%xrow(gfevdx,i))-gfevdx(i,i)
ewise fromvar(i)=%sum(%xcol(gfevdx,i))-gfevdx(i,i)
The calculation for the "generalized FEVD" done in the 2012 paper can be done by just feeding into ERRORS a factor matrix which isn't actually a factor of the covariance matrix. This produces a forecast "variance" for each series which is, in general, quite a bit higher than the actual forecast variance produced by the model. It's this higher value that is divided up among the shocks, so it still adds up to 100% across all shocks.
Sample Output
This is the output from a reduced set of returns (to keep the size manageable) with Cholesky shocks. A row represents a target variable, and a column represents a source shock. The numbers will (by construction) add up to 100 (subject to minor rounding) across a row. The "From Others" value at the end is the percentage that isn't due to "own" shocks. The "To Others" at the bottom is the sum down the column of the percentages that are from that shock to other target variables. The "From Others" column must sum to the same value as the "To others" row. The 37.7% is 226 divided by the overall total of 600 (100 per variable).
US UK FRA GER HKG JPN From Others
US 96.1 1.8 1.6 0.0 0.3 0.2 4
UK 40.6 57.5 0.8 0.4 0.1 0.5 42
FRA 38.5 22.7 38.6 0.1 0.0 0.2 61
GER 41.2 16.4 13.5 28.8 0.1 0.1 71
HKG 15.3 9.0 1.6 1.4 72.6 0.2 27
JPN 11.3 3.5 1.9 0.8 2.4 80.1 20
Contribution to others 147 53 19 3 3 1 226
Contribution including own 243 111 58 32 76 81 37.7%
In addition to the full sample tables, the papers include graphs of "rolling sample" estimates of the spillover measures. These involve moving sample estimates of the VAR's. For the 2009 paper, the window has 200 elements, which is roughly four years of weekly data. The graphed quantities are replaced with the missing value for those observations, which results in gaps (with sparse dots) in the graph. See, for instance, the middle of 2007 in the graph below.
compute nspan=200
set spillvols rstart+nspan-1 rend = 0.0
do end=rstart+nspan-1,rend
estimate(noprint) end-nspan+1 end
*
* Skip any data points where the rolling VAR has an explosive root.
*
eigen(cvalues=cv) %modelcompanion(volvar)
if skipUnstable.and.%cabs(cv(1))>=1.0 {
compute spillvols(end)=%na
next
}
compute gfactor=FactorMatrix()
errors(model=volvar,steps=nsteps,factor=gfactor,noprint,results=gfevd)
compute gfevdx=%xt(gfevd,nsteps)
ewise tovar(i)=%sum(%xcol(gfevdx,i))-gfevdx(i,i)
compute spillvols(end)=100.0*%sum(tovar)/%nvar
end do end
graph(footer="Spillover plot. Volatility. 200 week window. 10 step horizon")
# spillvols
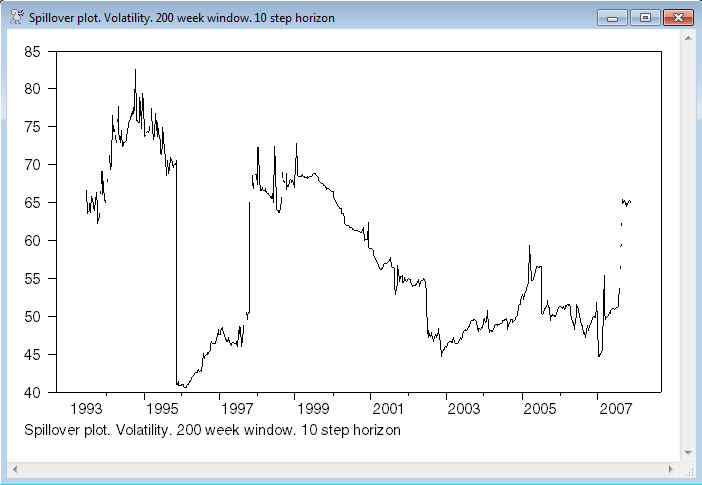
This is graphing the ten step total "TO" spillover measure. If you want to graph some other quantity (quantities), you need to set up the target series before the loop (here it was the SET SPILLVOLS instruction) and change the two COMPUTE's inside the loop to save the value you want. For instance, in this case, if you wanted the U.S. (variable 1) to France (variable 3) spillover measure, you would change this to something like
set us_to_fra rstart+nspan-1 rend = 0.0
and then
compute us_to_fra(end)=%na
when the sample is rejected and
compute us_to_fra(end)=100.0*gfevdx(3,1)
when it's accepted. (Again, the target is the first subscript and the source is the second in the GFEVDX array). You can, of course, compute multiple statistics by just doing multiple series like this. See, for instance, the later code with a width 75 window, which keeps both 2 and 10 step ahead results. The net spillover (which can be either positive or negative) between U.S. and France would be computed as something like
compute us_fra_net(end)=100.0*(gfevdx(1,3)-gfevdx(3,1))
(You would have to set up the US_FRA_NET series outside the loop).
If you want the total spillover to France specifically, after
ewise tovar(i)=%sum(%xcol(gfevdx,i))-gfevdx(i,i)
save the value of tovar(3) into the END entry of the series you are creating.
Copyright © 2026 Thomas A. Doan