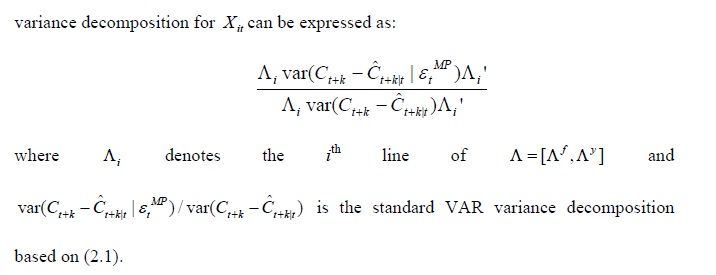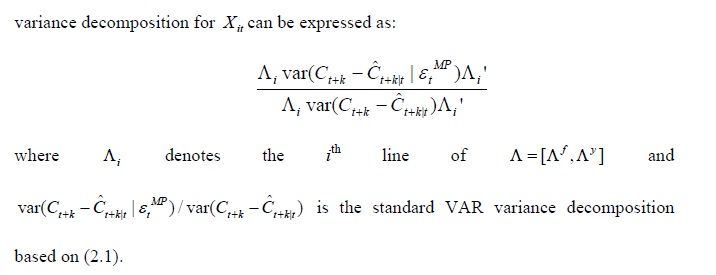The RATS Software Forum

Hi Tom,

I am wondering how the variance decomposition in a Factor Augmented VAR can be calculated based on the equation below.


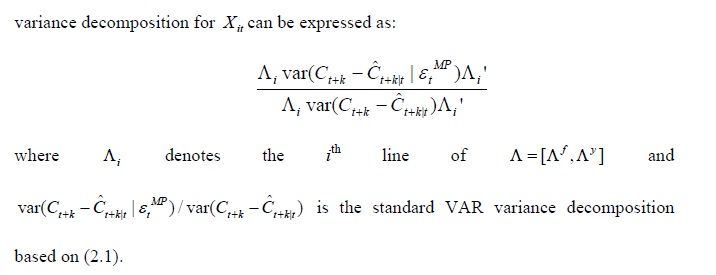
Source: Bernanke, Boivin and Eliasz (2003)

For example, I have a model ordered the following manner: Oil price, Activity factor (extracted from 50 variables), Price factor (extracted from 20 variables), and exchange rate. I allow variables in the activity factor to be a linear combination of oil price, activity factor, price factor and exchange rate. I am interested in the variance decomposition of GDP, which is in the activity factor. Wouldn't this just be multiplying the factor loading of GDP on each of these factors by the variance decomposition of each of these factors? That number is then divided by the overall variance that has been multipled by the loadings. But, that can result in a negative number?

Thanks.

Our replication file for BBE paper computes the variance decomposition.

If you're confused by the formula, you have a right to be. It makes no sense. The epsilon MP is never defined in the paper. If it means conditional on knowing the monetary policy shocks, then the first formula looks like it's the fraction that isn't explained, not the fraction that is. In the second formula, the var(C)'s are matrices, so you can't just divide them.

Hi Tom,

I had a look at the replication code. But, I am still struggling with the concept of variance decomposition in a FAVAR, partly also as I am very new to the program RATS.

Intuitively, I have always thought that the variance decomposition of variables within a factor can be computed in the following manner:

For example: GDP, M1, M2, GNE are explained by Factor 1. The factor loadings of GDP, M1, M2, GNE on Factor 1 are 0.2, 0.3, 0.2, 0.1.
The variance decomposition of Factor 1 explained by say a FFR shock is 40%. So, the variance decomposition of GDP is just a fraction of the variance decomposition of Factor 1, since these variables goes into the extraction of Factor 1.

I can get variance decomposition of the FAVAR variables. But, how do you get variance decomposition of the individual variables in each factor?

Would you be able to explain it further? Thanks.

FAVAR's are much more complicated than what you're describing. The basic calculation is the same as it is with a regular VAR---from a set of orthonormalized shocks, you compute impulse responses. The variance at horizon H for a variable is the sum across shocks of the sum from h=0,...,H-1 of the squares of the responses of a variable. The decomposition is given by the fraction of the sum due to each of the shocks.

Hi Tom,

If I understand your explanation correctly, would this be what you are saying?

For example, I have a simple model that has GDP, Factor 1, FFR. To get Factor 1, I have 10 variables that goes into that. Examples of the 10 variables are: CPI inflation, PPI inflation, Average wage earnings.
I am able to get the impulse responses (IR) of each variable due to each shock. For the variables within Factor 1, I am able to get the IRs via my observation equation.

If I want to get the variance decomposition of CPI inflation (which is a variable going into Factor 1) due to a shock in GDP at period 3, this is what I have to do:

[Sum of (IR of CPI inflation due to shock in GDP)^2 in Period 1 + 2/[(Sum of (IR of CPI inflation due to shock in GDP)^2 in period 1 + 2)+(Sum of (IR of CPI inflation due to shock in Factor 1)^2 in period 1 + 2)+(Sum of (IR of CPI inflation due to shock in FFR)^2 in period 1 +2)]*100

Apologies I am having to ask such basic stuffs on the internet. Most of my understanding on FAVARs have come from papers, that seem to assume you know everything. With this being a "relatively new" technique, it isn't covered in any of the textbooks I have come across as well. Thanks.

What do you mean by "I have 10 variables that go into that"? The BBE factor is latent---you can't construct it from other variables.

I meant to say that the unobserved factor 1 is extracted as the first principal component of the ten variables.

Would the variance decomposition I've described make any sense?

There are four shocks which hit one of those "X" variables: the three in the VAR, plus its own measurement error. Because the measurement error is assumed to be serially uncorrelated, that simply adds the measurement error variance to the denominator.

What you're describing would be the variance decomposition for 2-step-ahead forecasts.

[This post has been edited several times as I thought through things.]

Oh great! Then, that would be right, wouldn't it? I would then be able to get forecast error variance decompositions for H periods ahead.

Would you have any recommendations on textbooks or papers I could look into to have a better understanding of this type of models? I would really appreciate any references on this since everything I have come across so far assumes that the reader already knows the model.

I am still looking through the replication code. When I run it, I get a table of the variance decomposition, but with no title of each columns. I know that that is easily deciphered if I actually know the code and program well. Would you be able to tell me what are the missing titles of each of the columns in the variance decomposition part of the code? There are 5 columns in total excluding the first labels column. Are the first four columns the mean contribution of each shock (the three latent factors, and the FFR) to selected variables in the common component at the 60-month horizon? Is the last column the median for the R^2?

Is it absolutely necessary to "Compute means for the decomposition of variance for the common component (so they add up to 100%)" and "Compute median for the R**2"?

jacarandas wrote:[This post has been edited several times as I thought through things.]

Oh great! Then, that would be right, wouldn't it? I would then be able to get forecast error variance decompositions for H periods ahead.

Would you have any recommendations on textbooks or papers I could look into to have a better understanding of this type of models? I would really appreciate any references on this since everything I have come across so far assumes that the reader already knows the model.

Sorry, no. This is a very demanding type of model. You really have to be familiar with the static factor analysis literature first since the same issues of identifying the factors by restricting the loadings comes up. And, of course, any paper where a description of the Gibbs sampler runs to four pages isn't going to be for novices in handling simulation methods.

jacarandas wrote: I am still looking through the replication code. When I run it, I get a table of the variance decomposition, but with no title of each columns. I know that that is easily deciphered if I actually know the code and program well. Would you be able to tell me what are the missing titles of each of the columns in the variance decomposition part of the code? There are 5 columns in total excluding the first labels column. Are the first four columns the mean contribution of each shock (the three latent factors, and the FFR) to selected variables in the common component at the 60-month horizon? Is the last column the median for the R^2?

Yes. The first four divide up the "model"'s explained variance which is why they add to 100%. The last shows what percentage is covered by those four factors; 1-that is the percentage that's the measurement error.

jacarandas wrote: Is it absolutely necessary to "Compute means for the decomposition of variance for the common component (so they add up to 100%)" and "Compute median for the R**2"?

If you compute medians for the decomposition, they, in general, won't add up to 100%. Some people don't like how that looks.

If you compute medians for the decomposition, they, in general, won't add up to 100%. Some people don't like how that looks.

Thanks Tom. If possible, could I just ask a few more questions. I am understanding this much more than before.

Why would we need to compute the means for the decomposition of variance for the common component? What means are we talking about here? I was looking at the code and got a little confused. For example, I think this is what the code did:

- Get the variance decomposition of IP due to Shock 1, Shock 2, Shock 3, FFR shock.
- Get the mean of each of these variance decompositions and multiply them by 100. Then, the sum of these variance decompositions add up to 100% (which it should).

But, how do you actually get the mean of a single number? The variance decomposition of IP due to Shock 1 at the 60 month horizon would be a single number?

Also, presumably, if you add up the variance decomposition of a variable across shocks, it should add up to 100%? I guess I just wasn't too sure why do we need to compute the means.

With regards to the Rsquared (fraction of the variance of the variable explained by the common factors), I suppose this would really just be the squared of the impulse response of IP (say this is the variable I am interested in) divided by the sum of the squared impulse responses of the three factors?

There's a different set of responses for each Gibbs sweep so these are analyzing the distributions of the values across draws.

Even if f1(i)+f2(i)+f3(i)+f4(i)=100 for each i, if you compute medians across i for each component, they won't necessarily sum to 100. I don't have a problem with that, but some people do.

Yes, that's right! I have totally forgotten that this is conducted in a Bayesian framework. That explains why there is a need to take means to have it sum up to 100% and medians.

Thank you so much. Much appreciated.